Angles are everywhere! From the corners of your room to the way the hands on a clock move, angles play a significant role in how we see and interact with the world. If you’re just stepping into the world of geometry, understanding complementary angles is a great place to start. Not only are they a fundamental part of math, but they’re also surprisingly practical in daily life.
This blog will help you understand what complementary angles are, explore their properties, and discover real-world examples where they come into play. We’ve also included resources to continue your learning with fun, interactive tools.
What Are Complementary Angles?
Complementary angles are two angles that add up to exactly 90 degrees. Visualize a right angle (a perfect “L” shape)—now imagine splitting that 90° angle into two smaller angles. If their measures sum up to 90°, they’re considered complementary.
For example:
- A 30° angle and a 60° angle are complementary because 30° + 60° = 90°.
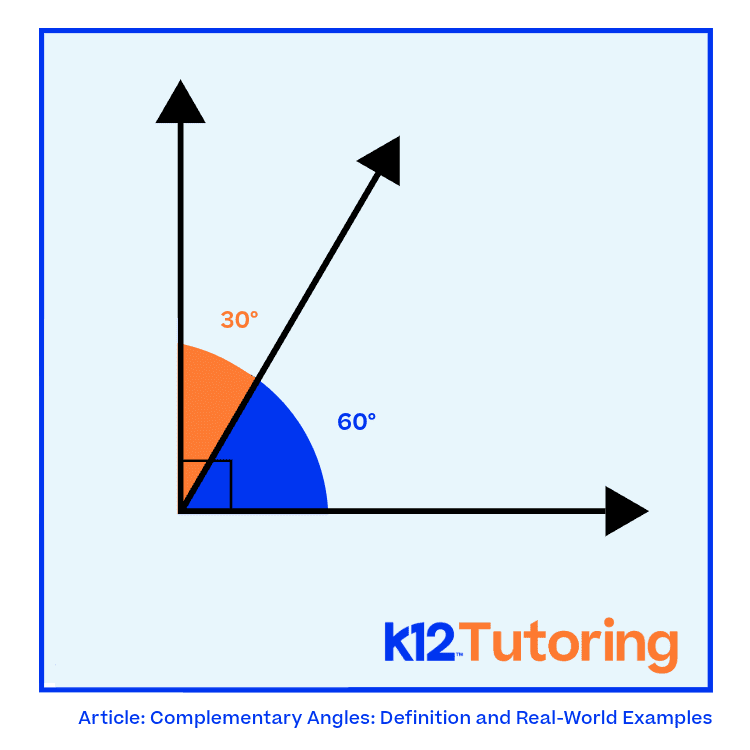
- Similarly, a 45° angle and another 45° angle are complementary because 45° + 45° = 90°.
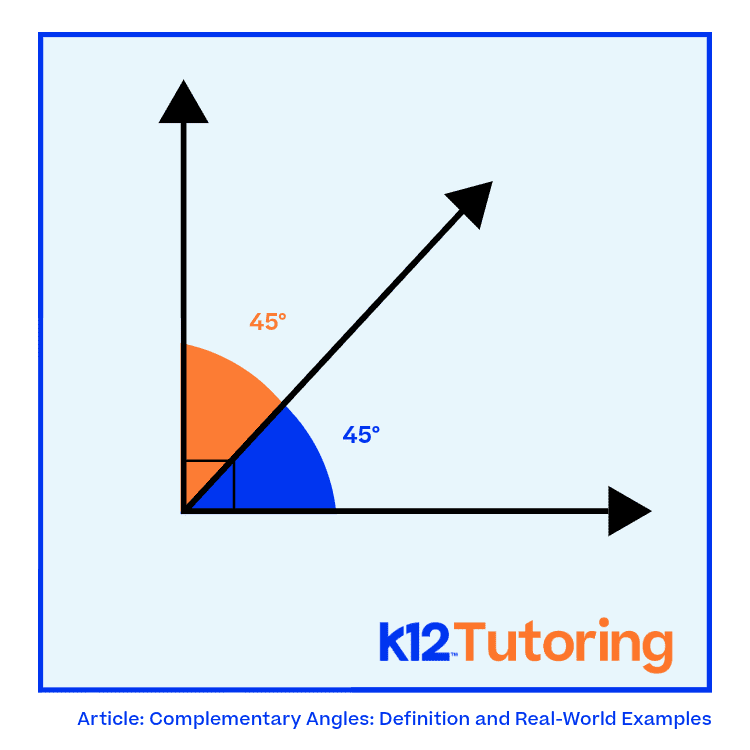
Key Properties of Complementary Angles
- They don’t have to be next to each other (adjacent). For example, one angle could be on your notebook while the other is on your friend’s notebook—they’re still complementary as long as their measures add up to 90°.
- Complementary angles can appear in various geometric shapes and designs, like triangles and rectangles.
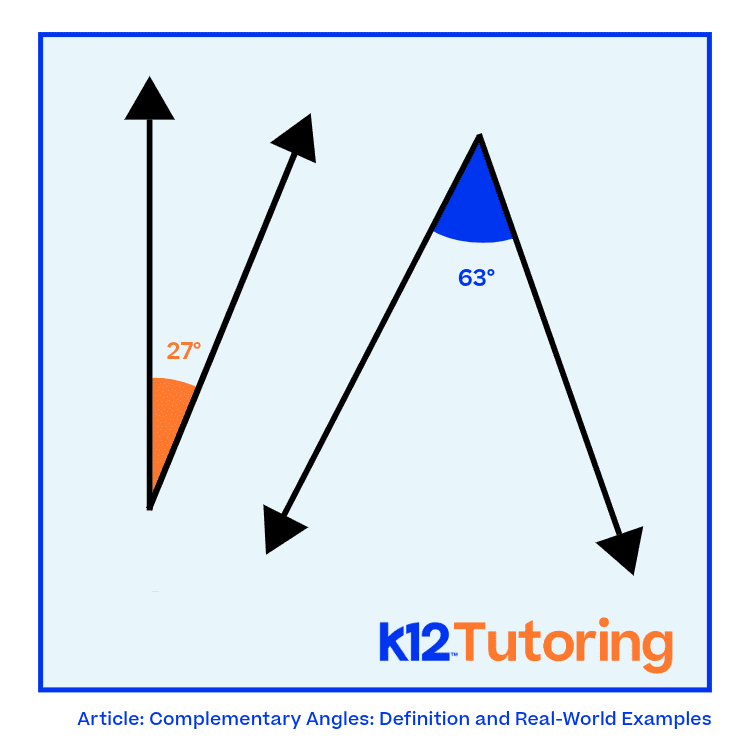
Knowing these properties is essential because complementary angles form the foundation for more advanced geometric concepts.
Real-World Examples of Complementary Angles
Complementary angles aren’t just limited to textbook diagrams—they’re evident all around us. Let’s look at a few real-world places where these angles show up:
1. Staircase Design
Take a look at a set of stairs. Each individual step usually involves a pair of complementary angles. The horizontal step (the tread) and the front vertical edge (the riser) often form a right angle. When a staircase is accurately designed, smaller angles (like the rise of the stairs) ensure structural balance and functionality.
2. Door Hinges
Ever noticed how doors open? The angle that the door makes with its frame often involves complementary angles. The hinge mechanism relies on these angles to allow for smooth and stable movement, especially in designs where part of the hinge creates a 90° rotation.
3. Street Corners
When crossing streets, you might encounter intersecting pathways that create complementary angles. Urban planners often use complementary angles to measure and map roads or intersections, ensuring the space is efficiently utilized.
4. Time on a Clock
Look at the hands of a clock when they form a right angle (like at 3 o’clock or 9 o’clock). The two smaller angles formed by the clock’s hands at these times are complementary because they add up to 90°!

If you’re a sports enthusiast, consider the way complementary angles are used in creating ramps at skate parks or the angles of soccer goalposts. Understanding these angles can help athletes optimize their performance, whether in launching a basketball or setting up a perfect golf shot.
Why Understanding Complementary Angles is Important
Understanding complementary angles isn’t just for acing geometry tests. Here’s why they matter:
- Practical Use: Architects, engineers, and designers rely on these angles to construct safe structures and functional systems.
- Foundation for Advanced Math: Complementary angles pave the way for learning trigonometry, calculus, and even physics concepts.
- Improved Problem Solving: Knowing how to spot and use complementary angles can boost your ability to analyze and solve real-world problems creatively.
Whether you’re adjusting your television mount or solving for missing angles in a geometry problem, this knowledge is a handy tool in your mental math toolkit.
Explore Further Learning Resources
Knowledge is like building a staircase—it grows with every step you take! If you’d like to enhance your understanding of complementary angles, check out these excellent online resources:
Khan Academy’s Complementary Angles Overview Lesson
Engage with interactive lessons and practice problems to boost your confidence in handling complementary angles.
GeoGebra’s Angle Exploration Tools
Visual learners will love exploring complementary angles dynamically with this hands-on tool.
Brilliant.org’s Bite-Sized Geometry Lessons
Build geometric skills in small, daily sessions with game-like progress tracking and interactive lessons that can be done on the go or at home.
These resources are perfect for both beginners and advanced learners who wish to solidify their understanding while having fun with math.
Wrapping Up
Complementary angles may seem like a small part of geometry, but their significance extends far beyond the classroom. From door hinges to staircases, they quietly shape the world around us. But remember, this is just the tip of the iceberg when it comes to geometry. There are countless other concepts to explore, from supplementary angles to trigonometric functions. So keep building on your knowledge and see where it takes you!
Want to keep exploring? Take the next step in your math adventure by checking out Khan Academy’s lessons or experimenting with visuals on GeoGebra. Gain a more thorough and in-depth explanation on angles with K12 Tutoring’s certified geometry tutors. You’ll be surprised at how much angles have to offer!





